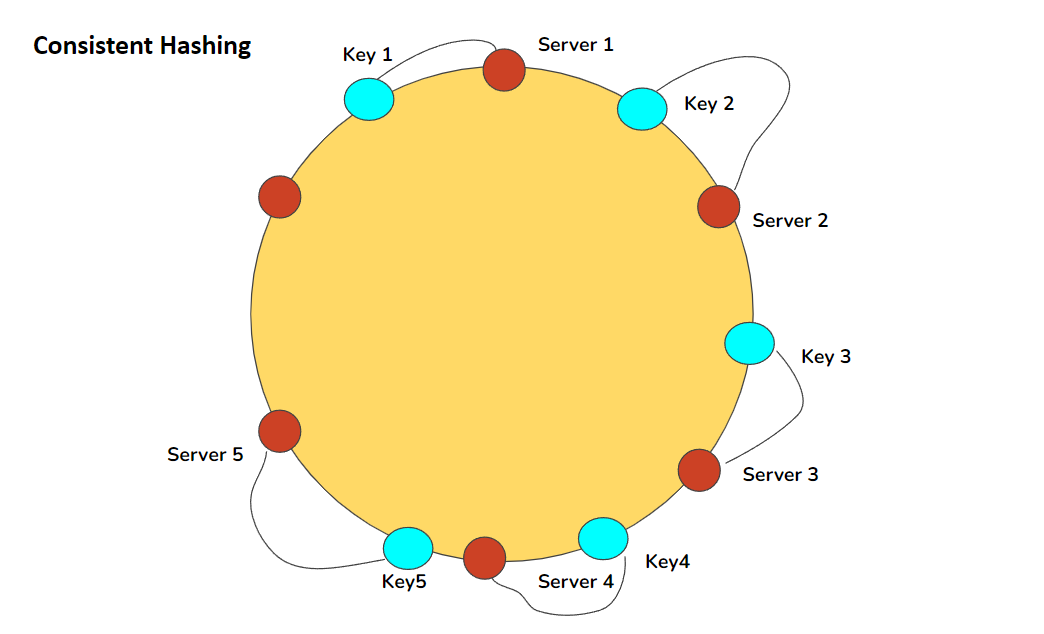
Consistent hashing is an important concept one should understand in order work with scalable system. Consistent hashing is used for distributing traffic evenly across servers. Lets understand in this article what consistent hashing is and how to design it.
Rehashing Problem
Consistent Hashing is a distributed hashing scheme that operates independently of the number of servers in a distributed hash table. A hash function is a function that maps one piece of data—typically describing some kind of object, often of arbitrary size—to another piece of data, typically an integer, known as hash code, or simply hash.
cacheServerIndex = hash(key)%N, N is the size of server pool
If there are 3 servers : A, B, C then as per the above hash function hash table would look like:
| KEY | HASH | HASH mod 3 |
|---|---|---|
| “ankit” | 1633428562 | 2 |
| “james” | 7594634739 | 0 |
| “akhil” | 5000799124 | 1 |
| “tanya” | 9787173343 | 0 |
| “zoya” | 3421657995 | 2 |
Now if user wants to retrieve server for key “ankit” then HASH%3 would be 2 i.e. server C. Similarly for others also these values can be retrieved.
This hash function is simple and distribution scheme also works fine until servers work properly and there’s no addition or deletion of servers. But in real world what if anyone of the servers crashes or goes down? Keys need to be redistributed in this case and account for the missing server. Same will be the case if new servers are added to the pool in this scenario keys need to be redistributed and account for newly added servers. This case will mostly be there for any distribution scheme but the problem here is with hash function hash modulo N which is dependent upon N. So, even if a single server changes, all keys will likely be rehashed into a different server.
In the previous above example if server C goes down then hash table would look like:
| KEY | HASH | HASH mod 2 |
|---|---|---|
| “ankit” | 1633428562 | 0 |
| “james” | 7594634739 | 1 |
| “akhil” | 5000799124 | 0 |
| “tanya” | 9787173343 | 1 |
| “zoya” | 3421657995 | 1 |
Now if you retrieve the server again for key “ankit” then HASH%2 will be 0 i.e. Server A, which no longer the same. Not just server “C” but all key locations have now changed. usually hashtable is stored inside cache, and as soon as the server count changes then on cache misses will occur as keys won’t be present in their old location and cache would need to retrieve data again from source to be rehashed, this would create load on the server and ultimately degrade the performance.
Solution : Consistent Hashing
This definition will now make more sense: “Consistent hashing is a distributed hashing scheme that operates independently of the number of servers or objects in a distributed hash table by assigning them a position on a hash ring.”
If we map the hash output range of above example onto the edge of the circle then this means minimum possible hash value, zero would correspond to angle of zero and maximum possible value(INT_MAX) would correspond to maximum angle of 2𝝅 radians i.e. 360 degrees and all the other hash values would fit somewhere in between. Assuming INT_MAX of 1010 then keys of our above example would look like:
| KEY | HASH | ANGLE (DEG) |
|---|---|---|
| “ankit“ | 1633428562 | 58.8 |
| “james“ | 7594634739 | 273.4 |
| “akhil“ | 5000799124 | 180 |
| “tanya“ | 9787173343 | 352.3 |
| “zoya“ | 3421657995 | 123.2 |

Now if we also placed servers on the edges of the circles by pseudo-randomly assigning them angles too. Done in a repeatable way or in a way that all clients agree on the server’s angles. One of the ways to do it would be using server name. With this change we have the following:

| KEY | HASH | ANGLE (DEG) |
|---|---|---|
| “ankit” | 1633428562 | 58.8 |
| “james” | 7594634739 | 273.4 |
| “akhil” | 5000799124 | 180 |
| “tanya” | 9787173343 | 352.3 |
| “zoya” | 3421657995 | 123.2 |
| “A” | 5572014558 | 200.6 |
| “B” | 8077113362 | 290.8 |
| “C” | 2269549488 | 81.7 |
As we have both keys for objects and servers in the same circle we can define a simple rule which will associate objects with servers. Each object key will belong in the server which is closest, in clockwise/counter-clockwise depending upon the convention used. Now, if you need to find out which which server to ask for a given key, you need to locate the key on the circle and move in ascending angle (counter-clockwise in this case) direction until a server is found.

| KEY | HASH | ANGLE (DEG) |
|---|---|---|
| “ankit” | 1633428562 | 58.7 |
| “C” | 2269549488 | 81.7 |
| “zoya” | 3421657995 | 123.1 |
| “akhil” | 5000799124 | 180 |
| “A” | 5572014557 | 200.5 |
| “james” | 7594634739 | 273.4 |
| “B” | 8077113361 | 290.7 |
| “tanya” | 787173343 | 352.3 |
| KEY | HASH | ANGLE (DEG) | LABEL | SERVER |
|---|---|---|---|---|
| “ankit” | 1632929716 | 58.7 | “C” | C |
| “zoya” | 3421831276 | 123.1 | “A” | A |
| “akhil” | 5000648311 | 180 | “A” | A |
| “james” | 7594873884 | 273.4 | “B” | B |
| “tanya” | 9786437450 | 352.3 | “C” | C |
How can you implement it? From implementation point of view what can be done is keeping a sorted list of server values (angles/numbers) and then search in this list the first server value greater than equal to the value of desired key. If no such element is found take the first value from the server list.
How can you ensure keys are evenly distributed among the servers?

| KEY | HASH | ANGLE (DEG) |
|---|---|---|
| “C6” | 408965526 | 14.7 |
| “A1” | 473914830 | 17 |
| “A2” | 548798874 | 19.7 |
| “A3” | 1466730567 | 52.8 |
| “C4” | 1493080938 | 53.7 |
| “ankit” | 1633428562 | 58.7 |
| “B2” | 1808009038 | 65 |
| “C0” | 1982701318 | 71.3 |
| “B3” | 2058758486 | 74.1 |
| “A7” | 2162578920 | 77.8 |
| “B4” | 2660265921 | 95.7 |
| “C9” | 3359725419 | 120.9 |
| “zoya” | 3421657995 | 123.1 |
| “A5” | 3434972143 | 123.6 |
| “C1” | 3672205973 | 132.1 |
| “C8” | 3750588567 | 135 |
| “B0” | 4049028775 | 145.7 |
| “B8” | 4755525684 | 171.1 |
| “A9” | 4769549830 | 171.7 |
| “akhil” | 5000799124 | 180 |
| “C7” | 5014097839 | 180.5 |
| “B1” | 5444659173 | 196 |
| “A6” | 6210502707 | 223.5 |
| “A0” | 6511384141 | 234.4 |
| “B9” | 7292819872 | 262.5 |
| “C3” | 7330467663 | 263.8 |
| “C5” | 7502566333 | 270 |
| “james” | 7594634739 | 273.4 |
| “A4” | 8047401090 | 289.7 |
| “C2” | 8605012288 | 309.7 |
| “A8” | 8997397092 | 323.9 |
| “B7” | 9038880553 | 325.3 |
| “B5” | 9368225254 | 337.2 |
| “B6” | 9379713761 | 337.6 |
| “tanya” | 9787173343 | 352.3 |
| KEY | HASH | ANGLE (DEG) | LABEL | SERVER |
|---|---|---|---|---|
| “ankit” | 1632929716 | 58.7 | “B2” | B |
| “zoya” | 3421831276 | 123.1 | “A5” | A |
| “akhil” | 5000648311 | 180 | “C7” | C |
| “james” | 7594873884 | 273.4 | “A4” | A |
| “tanya” | 9786437450 | 352.3 | “C6” | C |
How is this approach going to help when the number of servers change?
Suppose server “c” goes down, so all the labels C0…C8 will be removed from table and re-labelled & assigned to servers A and B randomly (Ax, Bx). All other keys of A and B servers will remain as it is and only the removed server keys will be reassigned to existing servers, thus existing keys are not disturbed in this approach.
Similar thing will happen if instead of removing a server you added a new server. Now roughly 1/number of existing server keys will be redistributed to the new server.
This is how consistent hashing works and how we solved rehashing problem with it.
Applications of Consistent Hashing:
- Maglev Network Load Balancer
- Discord Chat Application
- Akamai Content Delivery Network
- Data Partitioning across the cluster.