In a world that’s becoming increasingly digital, data privacy and security have taken the front seat. Breaches in data security can lead to significant losses, both financially and in terms of reputation. To combat this, end-to-end encryption (E2EE) has emerged as a robust solution for protecting sensitive data.

What is End-to-End Encryption?
End-to-end encryption (E2EE) is a method of secure communication that prevents third-parties from accessing data while it’s transferred from one end system or device to another. In E2EE, the data is encrypted on the sender’s system or device and only the recipient is able to decrypt it. Nobody in between, be they Internet service providers, hackers, or even the server that transmitted the data, can decrypt and read the data.
Why is End-to-End Encryption Required?
In our digital age, data is a precious commodity. Protecting this data from unauthorized access is crucial, especially when it involves sensitive information. This could be anything from personal conversations and photographs, to financial information and medical records. E2EE helps protect this data from digital eavesdroppers, ensuring only the intended recipient can access it.
Without E2EE, data while in transit can be intercepted and read by hackers or any third-party with access to the server through which data is being transmitted. With E2EE, even if a breach allows third-party access to the server, the data they find will be encrypted and unreadable, thus maintaining the privacy and integrity of the information.

HTTPS and Why It’s Not Enough
HTTPS, or Hyper Text Transfer Protocol Secure, provides a layer of protection by encrypting the data that is sent and received between a browser and a website. This ensures that the data cannot be read by anyone else who might intercept it during transmission.
However, HTTPS has its limitations. Firstly, it only protects data in transit, not data at rest or stored on servers. If the server is compromised, so is your data. Secondly, HTTPS does not encrypt metadata – information that describes other data. This can reveal who communicated with whom, when, and how often, which could be valuable information for advertisers or malicious actors.
Lastly, HTTPS relies on trusted Certificate Authorities (CAs) to verify the identities of websites. If a CA is compromised, or if they mistakenly issue a certificate to a fraudulent website, HTTPS cannot protect users from being misled and having their data intercepted.
In contrast, E2EE provides a higher level of security, protecting both the content and metadata, and not relying on any third-party for verification. It offers a much stronger, more comprehensive level of data security.
How Does End-to-End Encryption Work?
E2EE works by converting the original message into a coded message at the source (sender’s end) and then decoding it at the destination (receiver’s end). This ensures that even if the message is intercepted during transmission, it cannot be decoded and understood.
Let’s break down the process step by step:
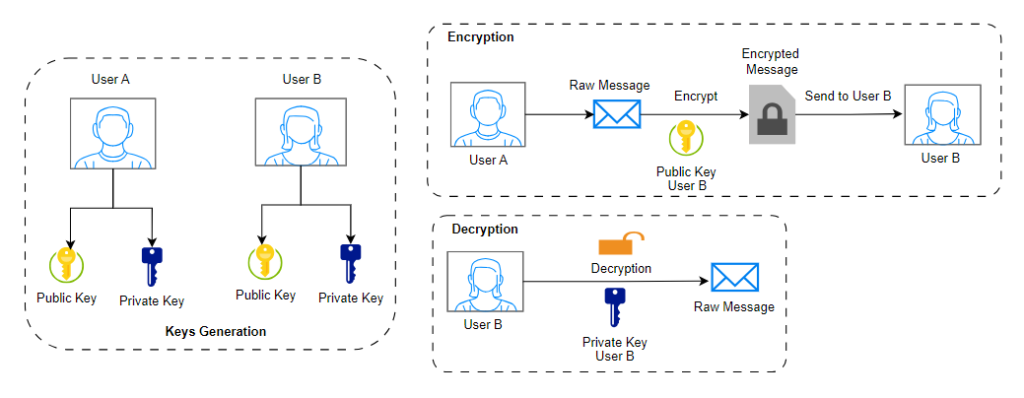
Key Generation: The first step in the E2EE process is key generation. Each user has a pair of cryptographic keys – a public key and a private key. The public key, as the name implies, is distributed to anyone who wishes to communicate with the user. The private key, on the other hand, is kept secret and only known by the user.
In Python, you can generate a pair of RSA keys using the `rsa` library like this:
```python
import rsa
(public_key, private_key) = rsa.newkeys(512)
```
Encryption: When someone wants to send a message, they encrypt it using the recipient’s public key. This forms a ciphertext – a scrambled version of the message that can only be decrypted using the correct private key.
Using Python’s `rsa` library, you can encrypt a message like this:
```python
import rsa
message = 'Hello, World!'
encrypted_message = rsa.encrypt(message.encode(), public_key)
```
Transmission: The encrypted message (ciphertext) is then sent over the internet. Even if this message is intercepted during transmission, it cannot be understood without the recipient’s private key.
Decryption: Once the message reaches the recipient, they use their private key to decrypt the message and read it.
In Python, you can decrypt a message using the `rsa` library like this:
```python
import rsa
decrypted_message = rsa.decrypt(encrypted_message, private_key).decode()
```
Verification: To ensure the integrity of the message, the recipient can verify it using the sender’s public key. This process ensures that the message was not tampered with during transmission.
Public and private keys are a fundamental part of secure communication, but real-world End-to-End Encryption (E2EE) involves more than just this basic key exchange. This section will explore various modern encryption algorithms that build upon this foundation. These algorithms include the Diffie-Hellman Key Exchange, Extended Triple Diffie-Hellman (X3DH), and the Double Ratchet algorithm.
The Diffie-Hellman Key Exchange Algorithm
The Diffie-Hellman Key Exchange Algorithm, formulated by Whitfield Diffie and Martin Hellman, is a widely recognized cryptographic protocol utilized to initiate a secure communication channel over insecure network. This protocol forms the foundation of numerous secure protocols in use today.
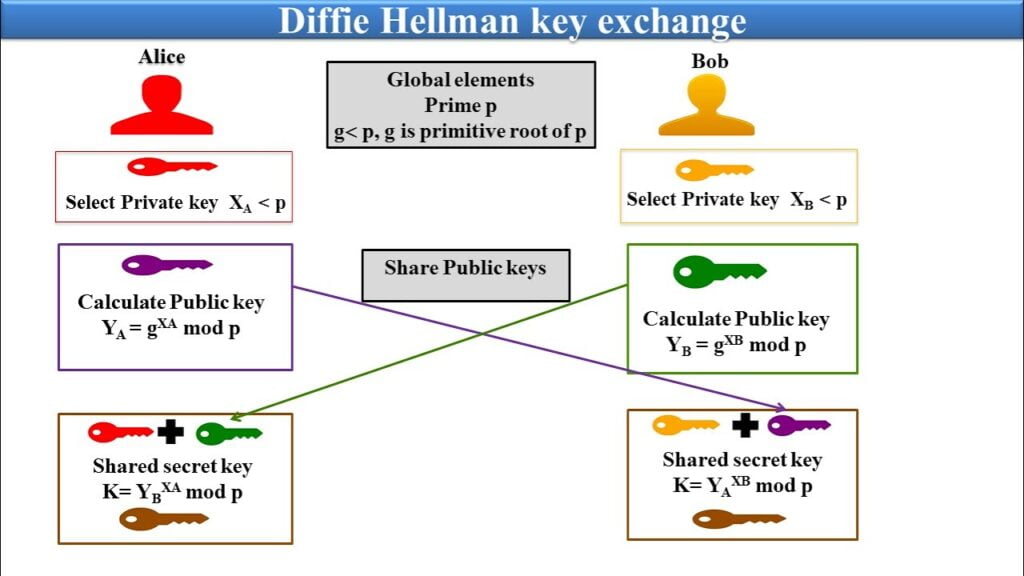
Let’s demonstrate the Diffie-Hellman Key Exchange Algorithm with characters Alice and Bob:
Key Generation: Initially, both Alice and Bob individually select a private key. This private key is essentially a random number that must remain confidential. They use this private key to generate their respective public keys. The formula `g^a mod p` is used to calculate the public key, where `g` is a known base number, `a` is the private key, and `p` is a known prime number. Both `g` and `p` are public.
Public Key Exchange: Alice and Bob exchange their public keys over the insecure network. Even if these public keys are intercepted, it is nearly impossible for an attacker to determine the private key from the public key.
Shared Secret Calculation: With each other’s public keys, both Alice and Bob can independently calculate the shared secret key. This is achieved by raising the received public key to the power of their own private key. For example, if Alice’s public key is `g^a mod p` and Bob’s private key is `b`, the shared key would be `(g^a mod p)^b mod p`. Similarly, if Bob’s public key is `g^b mod p` and Alice’s private key is `a`, the shared key would be `(g^b mod p)^a mod p`. These two results are identical due to the properties of modular arithmetic.
Secure Communication: Now, both Alice and Bob have the same shared secret and can use it as a symmetric key for encryption and decryption of messages between them.
To illustrate this process, let’s take an example. Suppose `g` = 2, `p` = 11, Alice’s private key (`a`) is 8, and Bob’s private key (`b`) is 3. Alice’s public key (`g^a mod p`) would be 3, and Bob’s public key (`g^b mod p`) would be 8. They exchange these public keys. Alice then computes the shared key as `8^8 mod 11` = 3. Bob also computes the shared key as `3^3 mod 11` = 3. Thus, they both end up with the same shared key, without ever transmitting it.
This way, despite being carried out over an insecure network, the Diffie-Hellman Key Exchange ensures the shared secret is never transmitted and independently computed by each party, making it impossible for an eavesdropper to figure out the shared secret from the public keys alone.
Extended Triple Diffie-Hellman (X3DH)
The Extended Triple Diffie-Hellman (X3DH) protocol is a key agreement protocol that provides end-to-end encryption. It’s used in applications like the Signal messaging app to ensure secure communication between two parties.
Here’s a step-by-step breakdown of how the X3DH protocol works, with a hypothetical example to illustrate the process:
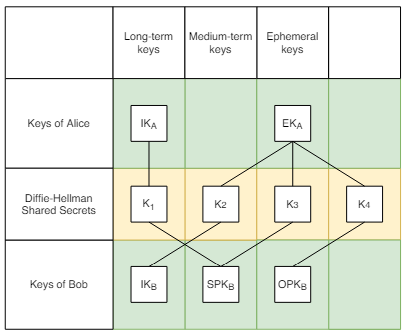
Key Generation: Alice and Bob, who wish to communicate securely, each generate three types of keys:
- Identity Key: A long-term public-private key pair that represents a user’s identity. For example, Alice generates an Identity Key pair (A, a) and Bob generates an Identity Key pair (B, b).
- Signed Prekey: A medium-term public-private key pair. The public key is signed by the Identity private key to ensure authenticity. Alice generates a Signed Prekey pair (S, s) and Bob generates a Signed Prekey pair (P, p).
- Ephemeral Key: A short-term public-private key pair that is generated for each new session. Alice generates an Ephemeral Key pair (E, e).
Key Exchange:
-Alice (initiator), who wishes to initiate a conversation, sends her Identity Key A and Ephemeral Key E to Bob.
-Bob (responder) responds with his Identity Key B, Signed Prekey P, and a bundle of Ephemeral Keys.
Diffie-Hellman Exchanges: Alice and Bob then perform three Diffie-Hellman exchanges:
– DH1: Between Alice’s Ephemeral Key E and Bob’s Signed Prekey P.
– DH2: Between Alice’s Ephemeral Key E and one of Bob’s Ephemeral Keys from the bundle.
– DH3: Between Alice’s Identity Key A and the same Ephemeral Key of Bob used in DH2.
Key Derivation: The shared secrets derived from the Diffie-Hellman exchanges are then concatenated and hashed to produce a single shared secret. This shared secret is used to encrypt and decrypt messages between Alice and Bob.
Message Encryption and Decryption: Alice and Bob can now use the shared secret to encrypt and decrypt messages. The encryption ensures that only the intended recipient can read the message.
The X3DH protocol provides forward secrecy, meaning that even if a user’s long-term keys are compromised, past communications remain secure. This is because the Ephemeral Keys, which are used to derive the shared secret, are deleted after use. In our example, even if Alice’s long-term keys are compromised, her past communication with Bob remains secure.
The Double Ratchet algorithm
The Double Ratchet algorithm, utilized for end-to-end encryption in instant messaging, incorporates the Extended Triple Diffie-Hellman (X3DH) key agreement protocol and a dual-action ratchet mechanism. This mechanism, which consists of a Diffie-Hellman ratchet and a symmetric-key ratchet, offers potent forward secrecy and future secrecy properties for the encrypted messages.
For a more detailed understanding, let’s consider a hypothetical scenario involving two communicators, Alice and Bob.
Initial Key Agreement: First, Alice and Bob establish a shared secret key through the X3DH protocol. This shared secret key is used to initialize the root key in the Double Ratchet algorithm.
Diffie-Hellman Ratchet: After Alice sends her first message to Bob, she generates a new ephemeral Diffie-Hellman key pair. She then includes the public part in her next message to Bob. Upon receiving Alice’s message, Bob uses his own key pair and the new public key from Alice to compute a new shared secret through a Diffie-Hellman calculation. This shared secret is then utilized to update the root key, thus providing forward secrecy.
Symmetric-Key Ratchet: Each message sent and received prompts an update in this ratchet, generating a new message key for each message and providing future secrecy. When Alice sends a message to Bob, she advances her sending chain key and derives a message key from it. Bob does the same with his receiving chain when he receives Alice’s message.
Key Derivation: The shared secret from the Diffie-Hellman calculation and the chain keys from the Symmetric-Key Ratchet are put into a key derivation function to produce the encryption and decryption keys.
Message Encryption and Decryption: Alice and Bob now have the message keys to encrypt and decrypt their messages, ensuring that only the intended recipient can read them.
Key Erasure: Once a message key has been used, it is immediately deleted. This ensures forward secrecy as the compromise of a current message key will not jeopardize the security of past messages.
Ratchet Update: The ratchets are updated after each message is sent or received. The Diffie-Hellman ratchet is updated with each round of communication, and the Symmetric-Key Ratchet is updated with each message.
In summary, the Double Ratchet mechanism guarantees that even if a single message key is compromised, past and future messages remain secure. This is referred to as future and past secrecy.
Conclusion
End-to-end encryption (E2EE) has emerged as a critical safeguard in our increasingly digital world. By encrypting data at the source and decrypting it only at the intended recipient’s device, E2EE offers a robust layer of security that surpasses what HTTPS can provide. This ensures that your sensitive information, from personal messages to financial records, remains protected from unauthorized access during transmission.
We explored the core principles of E2EE, including public and private key encryption, and witnessed its implementation through real-world examples like the Diffie-Hellman Key Exchange, Extended Triple Diffie-Hellman (X3DH), and the Double Ratchet algorithm. These sophisticated algorithms establish secure communication channels and continuously update encryption keys, ensuring forward and future secrecy for your data.
As we delve deeper into a digital age, the importance of E2EE will only magnify. By understanding its workings and embracing its use in our communication tools, we can empower ourselves to protect our privacy and navigate the digital landscape with greater confidence.